Wie lang ist die Spiral-Linie?
Auf einem Zylinder mit einem Durchmesser von einem Zentimeter und zehn Zentimetern Höhe
verläuft eine spiralförmige Linie, die den Zylinder genau fünfmal umrundet.
Können Sie die Länge dieser Linie ermitteln?

Lösung
Da die Spiral-Linie dreidimensional ist, empfiehlt sich zur
Berechnung zunächst ein Blick auf die Abwicklung.

Wenn die Spiral-Linie den Zylinder fünfmal umrundet, muss die Breite dem fünf-fachen der Länge entsprechen.
Mit dem Satz des Pythagoras (a2 + b2 = c2) lässt sich nun die Diagonale
dieses Dreiecks in einer einfachen Wurzelgleichung darstellen.
Länge der Spiral-Linie = 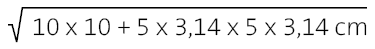
Länge der Spiral-Linie =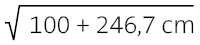
Länge der Spiral-Linie = 18,6 cm
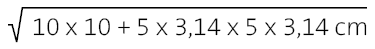
Länge der Spiral-Linie =
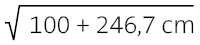
Länge der Spiral-Linie = 18,6 cm
Abonnieren Sie das Magazin Luftfeuchte für monatlich aktuelle Technik-News und Nützliches aus der TGA-Praxis.